Per l’acquisizione del senso del numero: quale retta numerica ?
Su tutti i libri di matematica della Scuola primaria campeggia la retta numerica. L’ape Serafina è affascinante quando produce salti immaginari per andare a succhiare il dolce nettare dai fiori. Il compito per gli alunni è però più complicato di quanto appaia nella storia immaginaria dell’animaletto.

La classica linea dei numeri si configura come una retta numerica frammentata da barrette numerate.
Scopriamo, ma lo scoprono prima di noi bambini, che non dobbiamo calcolare le quantità, ma gli spazi vuoti. Ogni quantità, intesa come spazio vuoto, ha un confine destro e sinistro contraddistinto da un numero. Ad esempio il numero due inteso come spazio si trova a destra o a sinistra del numero detto?
I bambini fino a questo momento e già prima di arrivare a scuola possiedono la connotazione semantica e lessicale del numero, ma non avendo dimestichezza con i simboli scritti essi sono abituati a trattare con biscotti palline, fiori; ora devono sommare o sottrarre spazi vuoti.
Lo zero, cioè il nulla, si è inserito nel rendiconto analitico delle quantità.
L’ambito semantico è l’ambito delle immagini-emozioni.
Butterworth afferma che già dalla nascita abbiamo una natura predisposta per conoscere il mondo in termini quantitativi; le difficoltà nel contare dei bambini piccoli, per l’autore, dipendono dalle difficoltà dell’apprendimento dei vocaboli, e più oltre dalla posizione dei simboli numerici.
Per l’acquisizione dei fatti numerici non facilitano la comprensione ragionamenti o intellettualizzazioni. Il segreto per una più facile opera di insegnamento sta nel cercare di scoprire come si formano nella mente le immagini del numero, oltre l’applicazione della logica adultistica.
Butterworth ritiene che di fronte ad una quantità numerica, bambini ed adulti riescono a contare gli oggetti trasformandoli in una immagine interna fugace e transitoria, assecondando il tempo del respiro che è di tre secondi e che quindi solo tre oggetti possono entrare nello schermo biologico. Subito dopo la percezione crolla.
Gelman e Gallistel hanno studiato lo sviluppo del concetto di numero ed in questa sede ci interessa, di tale studio, approfondire il processo di astrazione che riguarda la formazione delle rappresentazione di numerosità, approssimate o precise delle collezioni; esso comprende il “subitizing” o subitizzazione: processo rapido, senza sforzo inconsapevole con cui si stabilisce con accuratezza la numerosità di insiemi di dimensioni limitate, da 1 a 3-4 elementi.
Secondo Butterworth se vediamo tre mucche in un prato capiamo che sono tre ancora prima di capire che si tratta di mucche. Per facilitare, allora, la capacità dello schermo biologico , ci serve uno spazio integrale provvisto di pieno e vuoto; ci servono immagini analogiche che ci permettano un subitizing immediato che vada oltre il numero tre. Gli studi di Jean Piaget e Jerome Bruner ci hanno fatto comprendere che i bambini, prima di sei anni, pensano che oggetti che variano la loro posizione nello spazio variano anche la loro numerosità. Per superare tale con concezione “magica”, se vogliamo “conservare le quantità” nella mente, sarà necessario disporre gli oggetti da contare con un ordine stabile.
Facciamo alcuni esempi di quantità ordinate:
Tale disposizione non contiene nessuna simmetria.

Questa disposizione invece contiene troppa simmetria.
.
In quest’ultima disposizione appare un piccolo scarto di simmetria e per questo il conteggio è favorito.
Questo tipo di disposizione lo ricaviamo dalla disposizione delle dita allineate e lo spazio vuoto al centro si riferisce allo spazio tra una mano all’altra.
La linea del 20, del 100, del 1000 di Camillo Bortolato abitua il bambino, sia attraverso le tastierine, sia attraverso rappresentazioni grafiche, che attraverso i software, ad uno scorrimento di etichette sulla linea dei numeri che dà luogo ad una serie infinita di ordinalità e cardinalità provvisoria a seconda del conteggio che scegliamo. Il metodo analogico, quindi, è il metodo del silenzio, dell’istantarietà, della simulazione che sostituisce le inutili spiegazioni verbali con l’impegno di liberarsi dalla forma di pensiero che identifica il calcolo con il risultato di un’attività di ragionamento; quest’ultimo è sostituito dal conteggio basato sulla percezione, per allungare quel colpo d’occhio quale schermo biologico che dura tempo di un respiro e questa volta con numeri che vanno lotre il tre…
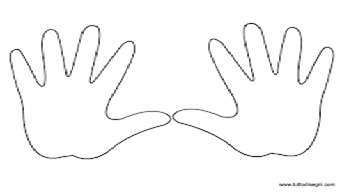
Esercitazioni orali su “La linea del 100”
Consegna: cerca con gli occhi i numeri che ti indicherò.
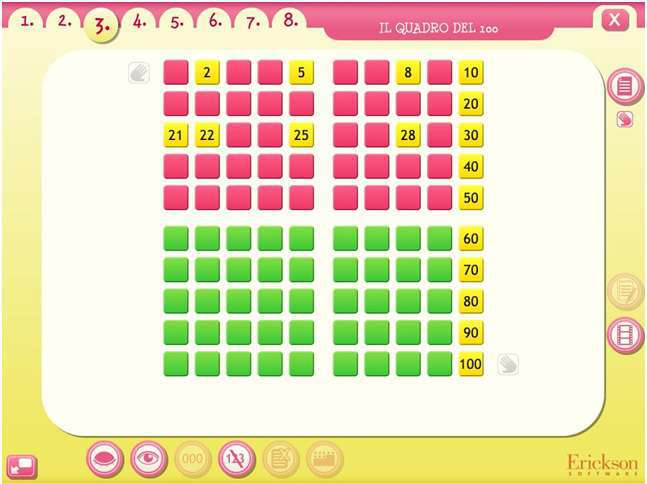
Un esempio di calcolo orale, e poi registrato, fatto sulla linea dei numeri con riferimento alla logica di Camillo Bortolato.

Butterworth B., (1999), The mathematical brain. Trad. It.
Intelligenza matematica. Milano, Rizzoli. 1999
Camillo Bortolato 2006 Metodo analogico per l’apprendimento del calcolo, Trento Ed. Erickson
Camillo Bortolato LIM Matematica analogica
Lucangeli D. – Poli S. – Molin A. (2003), L’intelligenza
numerica. Tento Ed. Erickson
Miceli S. S. (2002), La conservazione della quantità
nell’insegnamento/apprendimento della matematica retta numerica (età 5-6
anni).
Piaget J. – Szeminska A.(1941), La genèse du nombre chez
l’enfant. Neuchâtel, Delachaux et Niestlé, .Trad. It. La genesi del
numero nel bambino. Firenze, La Nuova Italia,1968

