La matematica è una materia complessa ed articolata e i suoi teoremi richiedono lo svolgimento di diverse operazioni, tra cui quello della radice quadrata.
Tuttavia, prima di studiarle, a scuola viene prima insegnato il funzionamento delle potenze, poiché esse ne costituiscono il principio basilare. Infatti, calcolare la radice quadrata significa capire quale numero elevato al quadrato (cioè “alla seconda”) ci farà ottenere la quantità posta sotto la radice.
Come ben sappiamo, in matematica non esistono solo le radici quadrate, ma sono molto conosciute anche quelle cubiche (o “alla terza”). Ad ogni modo, il loro calcolo è una delle operazioni più semplici… se fatte con la calcolatrice!
Ma senza?
Oggi vedremo appunto come calcolare la radice quadrata senza calcolatrice
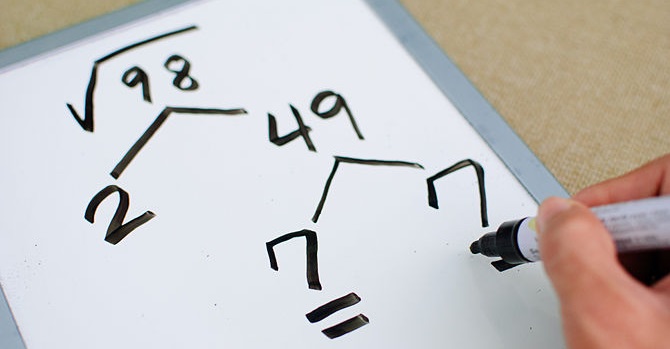
Innanzitutto, dobbiamo dire che la radice è composta da diversi elementi: il numero che sta sotto la radice è chiamato radicando, in alto a sinistra della radice si trova l’indice mentre a destra della radice vi è ovviamente il risultato!
Iniziamo con il prendere in esame i numeri più semplici: i quadrati perfetti. Vengono chiamati così perché di tali numeri non occorre calcolare la radice: ad esempio, la radice quadrata del numero 9 è 3, poiché 3^2=9 (il simbolo ” ^ ” si legge “elevato”); la radice quadrata del numero 16 è 4, la radice quadrata di 49 è 7….e così via.
Per i quadrati non perfetti, invece, bisogna distinguere due tipi di numeri: i numeri composti da due cifre e quelli composti da tre o più cifre. Per quelli composti da due cifre, tutto quello che dovete fare è trovare quel numero che moltiplicato per se stesso si avvicini più possibile al radicando. Ad esempio, se dovessimo eseguire la radice quadrata di 43, potremmo subito dire che la soluzione è 6, perché il quadrato di 6 (36) è quello che si avvicina maggiormente a 43 senza superarlo. Ovviamente, il risultato risulterebbe approssimato: per continuare con il calcolo dovrete aggiungere al radicando uno zero e la virgola al risultato.
Se il numero è invece composto da due o più cifre, dovrete mettere un punto ogni 2 cifre partendo da destra e proseguendo verso sinistra, come se voleste suddividere il numero in “blocchi” (ad esempio, 47689 verrà diviso e scritto come 4.76.89).
Ora, partendo da sinistra, dovrete cercare un numero che elevato al quadrato sia uguale o si avvicini alla cifra del primo “blocco”. Unite il numero da voi scelto a destra del simbolo del radicale ed eventuale resto sotto il numero del “primo blocco”. Adesso dovrete “abbassare” le cifre del secondo numero, cioè scriverle accanto al resto prima ottenuto (anche se uguale a zero). Prendete ora la prima cifra della radice (che avete segnato prima a destra), raddoppiatela ed aggiungetevi un numero che vada da 0 a 9, poi moltiplicate questo numero per la stessa cifra (quindi se la vostra radice fosse ad esempio 2, raddoppiatela e diverrà 4; aggiungete al 4 un numero che va da 0 a 9, ad esempio 5, ottenendo il numero 45, che verrà moltiplicato per 5. Se scegliete il numero 6, otterrete 46 x 6, nel caso sceglieste 7, sarà 47 x 7 e così via). La cifra che avrete ottenuto con la moltiplicazione…..dovrà avvicinarsi il più possibile (o essere totalmente uguale) al numero che stiamo cercando.
Approssimazione
Ricordate che la radice, come tutti i calcoli matematici, potrà essere approssimata. Spetterà a voi scegliere se calcolarne i decimali, usando la virgola e gli zeri, o calcolarne la radice intera, lasciando il resto. L’approssimazione può essere fatta per difetto, ovvero prendendo in considerazione il numero intero che precede il risultato, oppure per eccesso, prendendo l’intero che segue immediatamente il risultato o radicando. Tuttavia, in entrambi i casi, possiamo approssimare a meno di un decimo (0,1), a meno di un centesimo (0,01), a meno di un millesimo (0,001) ecc. Ovviamente, maggiori decimali significheranno un’approssimazione più esatta.
